1. 개요
지난주에 받은 질문 중 '재귀함수 자세히 공부 안 해도 되지 않나요? 어차피 많이 안 쓴다던데'라는 질문이 있어 글을 작성한다.
저 질문을 받았을 때 '재귀함수 쓰니까 공부해야된다'고 대답했다.
그런데 저 질문이 무슨 맥락에서 나온건지 알고 있다.
사실 재귀함수는 반복문에 비해 비효율적이고, 그래서 잘 안 쓰는 게 맞다.
그럼 저 질문이 맞는 거 아닌가?라고 생각할 수 있지만, 그래도 재귀함수는 알아야 한다.
단순히 잘 쓰지 않는다는 결과만 볼게 아니라 그 과정을 이해해야 한다.
1) 재귀함수는 반복문에 비해 비효율적이기 때문에 일반적인 상황에서는 반복문을 사용한다.
2) 하지만 재귀함수를 써야 되는 상황이나 재귀함수를 쓰면 훨씬 간단하게 코드를 작성할 수 있는 경우가 있다.
3) 위와 같은 재귀함수를 써야되는 상황에서 비효율적이라는 단점을 극복하는 방법이 있다.
위 세 과정을 이해하기 위해서는 재귀함수의 작동 방식을 알아야 하고, 특히 2번과 3번을 위해서는 본인이 재귀함수를 사용할 수 있어야 한다.
그래서 이번 글에서는 위 세 과정에 대해 설명해보려고 한다.
재귀함수의 동작과정을 이해하기 어려워하는 사람이 많아 우선 재귀함수가 뭔지 설명할 것이다.
그다음 for문과 재귀함수를 비교해 보며 재귀함수가 필요한 상황을 알아볼 것이다.
그 후 재귀함수의 단점을 극복하는 방법을 소개하려고 한다.
2. 재귀함수(Recursion)
2.1. 정의
재귀함수란 자기 자신을 다시 호출하는 함수다.
일반적인 함수는 자신이 해야 할 명령을 수행하고 나면 종료된다.
그런데 함수가 작동하는 중에 자기 자신을 호출하면 함수가 한번 더 실행되도록 할 수 있는데, 이것을 재귀함수라고 한다.
다음은 재귀함수의 예시로 가장 많이 사용되는 팩토리얼이다.
참고로 4팩토리얼은 4 * 3 * 2 * 1로 24가 나온다.
코드 :
#include <stdio.h>
int factorial(int n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
}
int main() {
int n = 4;
printf("%d", factorial(n));
}
실행과정:

결과 :

2.2. 작동방식
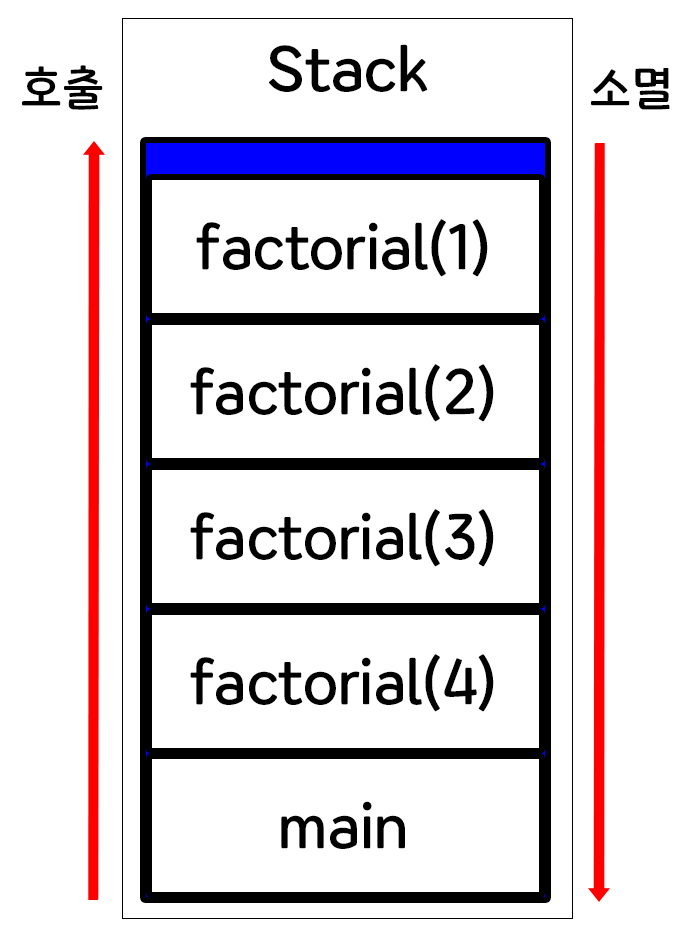
재귀함수는 함수를 여러 번 호출한다.
이때 호출된 함수의 데이터는 메모리의 스택영역에 쌓인다.
그리고 스택영역은 후입선출방식, 즉 늦게 들어온 데이터가 먼저 소멸된다.
그러므로 나중에 호출된 함수가 먼저 끝나고 사라진다.
2.3. 주의점
재귀함수는 반드시 종료조건이 필요하다.
만약 재귀함수의 종료조건이 없으면 함수가 계속 자기 자신을 호출하게 되고, 그 데이터가 스택에 계속 쌓이게 된다.
그렇게 되면 메모리가 정해진 스택영역을 뚫고 나가는 Stack overflow 에러가 발생한다.

3. 재귀함수가 비효율적인 이유
재귀함수가 비효율적인 가장 큰 이유는 메모리의 낭비가 심하기 때문이다.
앞서 재귀함수는 스택영역에 메모리를 계속 쌓는다고 설명했다.
그 말은 재귀 횟수가 늘어날수록 사용해야 할 스택영역의 크기가 늘어나야 한다는 것이다.
그런데 보통 스택영역의 크기는 생각보다 작다.
그래서 종료조건이 있더라도 재귀 횟수가 많으면 stack over flow를 발생시킬 수 있다.
그게 아니더라도 재귀함수가 실행되며 당장 사용하지 않을 불필요한 자원을 너무 많이 차지한다.

위 사진과 같이 재귀함수는 실행 횟수에 따라서 차지하는 메모리가 점점 커진다.
그리고 당장 실행되는 부분을 제외한 나머지는 함수가 return 되기만을 기다리는 불필요한 부분이다.
반면에 for문은 반복 횟수가 늘어나도 사용하는 메모리의 크기는 정해져 있다.
한정된 메모리 내에서 정해진 횟수만큼 반복하기 때문에 메모리관점에서 훨씬 효율적이다.
그래서 for문으로 간단하게 해결할 수 있다면 for문을 쓰는 게 낫다.
4. for문과 재귀함수 비교
다음은 for문과 재귀함수를 비교해 보겠다.
위에서 팩토리얼을 재귀함수로 구현했지만, 사실 for문으로 작성하는 것도 간단하다.
코드 :
#include <stdio.h>
int factorial(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
int main() {
int n = 4;
printf(" %d\n", factorial(n));
}
재귀함수를 처음 배우는 사람들은 쓰기도 어렵고 단점도 큰 재귀함수를 왜 쓰는지 이해가 되지 않을 것이다.
위 팩토리얼처럼 재귀함수로 구현할 수 있는 대부분은 반복문으로 대체가 가능하다.
그럼 재귀함수는 어떤 상황에서 쓰이는 것일까
이제 재귀함수의 작동방식을 어느 정도 이해했으니 재귀함수가 필요한 사례를 설명하겠다.
4.1. 재귀함수가 필요한 이유
문제 :
1부터 n까지의 정수를 3번 나열할 수 있는 모든 경우를 출력하라.
입력 :
3
출력 :
1 1 1
1 1 2
1 1 3
1 2 1
...
3 3 3
먼저 위 문제를 for문과 배열을 이용해 구현해 보겠다.
코드 :
#include <stdio.h>
int main() {
int n, arr[10];
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
arr[1] = i; // 배열의 각 자리에 1부터 n까지 대입
for (int j = 1; j <= n; j++) {
arr[2] = j;
for (int k = 1; k <= n; k++) {
arr[3] = k;
printf("%d %d %d\n", arr[1], arr[2], arr[3]); // 출력
}
}
}
}
아마 재귀함수를 배울 때쯤이면 이 정도는 어렵지 않게 구현할 수 있을 것이다.
그런데 이 방식은 문제에서 3번이 아니라 6번 나열하라고 하면 for문을 6개, 10번이면 for문도 10개를 사용해야 할 것이다.
조금 더 최적화시킬 수 있지만, 그것도 고정 횟수가 아니라 M번 반복하라고 하면 코드가 더 복잡해질 것이다.
참고 코드 :
#include <stdio.h>
int n, m, arr[10];
void output() {
for (int i = 1; i <= n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
arr[i] = 1;
}
int done = 0; // 모든 경우의 수를 확인했는지 여부
while (!done) {
output();
done = 1;
for (int i = n; i >= 1; i--) {
arr[i] += 1;
if (arr[i] <= m) {
done = 0;
break;
}
else arr[i] = 1;
}
}
}
하지만 재귀함수를 사용하면 이 코드를 더 간단하게 구현할 수 있다.
코드 :
#include <stdio.h>
int n, arr[10];
void output() {
for (int i = 1; i <= 3; i++) {
printf("%d ", arr[i]); // 5. 출력
}
printf("\n");
}
void recursion(int step) {
if (step > 3) {
output(); // 4. step이 3번 반복됐으면 output 실행
return;
}
for (int i = 1; i <= n; i++) {
arr[step] = i; // 2. 배열의 각 자리에 1부터 n까지 대입
recursion(step + 1); // 3. 다음 step 실행
}
}
int main() {
scanf("%d", &n);
recursion(1); // 1. 첫번째 step 실행
}
위 코드는 재귀함수를 반복하며 실행된다.
위처럼 작성하면 3번이 아니라 M번이 되더라도 문제없이 작동된다.
이렇게 for문으로 작성하면 복잡해지는 코드를 간결하게 작성할 수 있다는 장점 때문에 재귀함수를 사용한다.
5. 꼬리재귀(Tail call recursion)
하지만 앞서 말했듯 재귀함수는 반복문보다 비효율적이기 때문에 재귀함수를 쓰면서 성능저하를 일으키지 않을 방법이 필요해졌다.
그래서 나온 방법이 꼬리재귀이다.
기존 코드 :
#include <stdio.h>
int factorial(int n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
}
int main() {
int n = 4;
printf("%d", factorial(n));
}
처음 봤던 예시인 팩토리얼 재귀함수 코드이다.
이 코드는 메모리에 기존 함수를 유지하며 다음 스택의 함수를 실행시켜 성능 저하를 일으킨다.
그런데 꼬리재귀는 다음 함수를 실행할 때 기존 함수가 차지하던 메모리를 그대로 사용한다.
꼬리재귀 코드 :
#include <stdio.h>
int factorial(int n, int m) {
if (n <= 1) return m;
return factorial(n - 1, n * m);
}
int main() {
int n = 4;
printf("%d", factorial(n, 1));
}
이전 코드와의 차이점은 return부분에 연산이 없다는 것이다.
이렇게 코드를 작성하면 다음 스택이 실행될 때 이전 스택 함수가 실행되던 자리를 그대로 사용하도록 컴파일러가 최적화시킨다.
한마디로 호출스택을 새로 생성하지 않는다는 것이다.
결과적으로 for문을 사용했을 때와 큰 차이가 없게 된다.
6. 마무리
마지막 꼬리재귀 파트에서 정말 메모리를 그대로 사용하는지까지 적으려고 했는데 글이 너무 길어지고, 따로 글을 작성하자니 별거 없는 내용이라 방법만 적어두려고 한다.
우선 컴파일러가 최적화를 지원해야 한다.
Visual studio의 경우
1) 프로젝트 속성 - C/C++ - 최적화 - 최적화 - 최적화(속도 우선)(/Ox) 으로 설정
2) C/C++ - 코드 생성 - 기본 런타임 검사 - 기본값 으로 설정
이러면 최적화가 진행된다.
그런데 이렇게 하면 함수가 실행되는 게 잘 보이지 않아 함수 내부에 중단점을 걸고 한 단계씩 실행하며 스택이 어떻게 바뀌는지 확인해야 한다.
틀린 내용이 있으면 댓글로 적어주세요
출처 :
https://en.wikipedia.org/wiki/Recursion_(computer_science)
'생각 정리' 카테고리의 다른 글
| 컴퓨터의 덧셈과 뺄셈 (0) | 2024.05.30 |
|---|---|
| 레퍼런스 변수와 포인터 변수 (0) | 2024.04.29 |
| 배열 (0) | 2024.04.22 |
| 포인터 연산 (0) | 2024.04.21 |
| 포인터 (0) | 2024.04.14 |


